
| ROTATIONS ABOUT THE ORIGIN |
Introduction
In geometry, a rotation is a transformation that changes the position of a figure
in the plane by turning it about a point called the center of rotation.
The degree measure of the turn is called the angle of rotation.

The hands of a clock rotate clockwise (of course!) about the center of the clock's face as time passes. The big (minute) hand turns through 360° every hour, the little (hour) hand rotates 1/12 of that or 30° every hour whereas the second hand races around doing a 360° turn every minute!
Notice how we define a rotation with 3 pieces of information:
1. the orientation (clockwise),
2. the center point, and
3. the angle of rotation.
Though we can rotate any two dimensional figure about any point in the plane through any angle, we usually begin our study of rotations with multiples of 90° about the origin.
.
Rotations about the Origin: (multiples of 90°)
Let's look at the changes in a figure's vertex coordinates under rotations of 90°, both counterclockwise and clockwise.
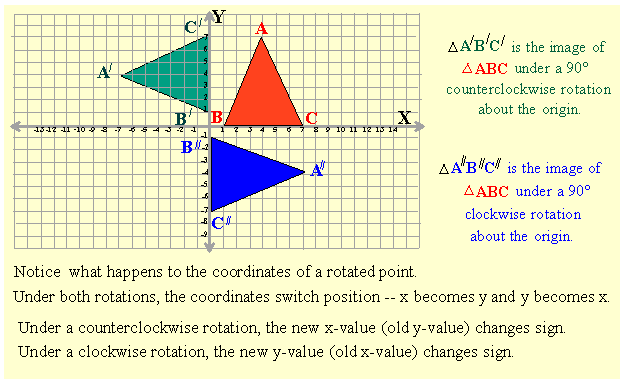
Notice how under a counterclockwise rotation of 90° about the origin:
| A(4, 7) became A/ (- 7, 4) | B(1, 0) became B / (0, 1) | C(7, 0) became C / (0, 7) |
Since 0 is neither positive nor negative, we don't see the change in sign, however, in point A we can see it. The reason the x-value changes sign is that under a counterclockwise rotation, we move the figure from right of the y-axis to left of it. Had our figure started out left of the axis, it would've ended up on the right side, so again, the sign of the first coordinate -- x -- has to change.
Notice also how under a clockwise rotation of 90° about the origin:
| A(4, 7) became A/ (7, - 4) | B(1, 0) became B / (0, - 1) | C(7, 0) became C / (0, - 7) |
The reason the y-value changes sign is that we move the figure from above the x-axis to below it. Had our figure started out, below the axis, it would've ended up above it, so again, the sign of the second coordinate -- y -- will change.
.
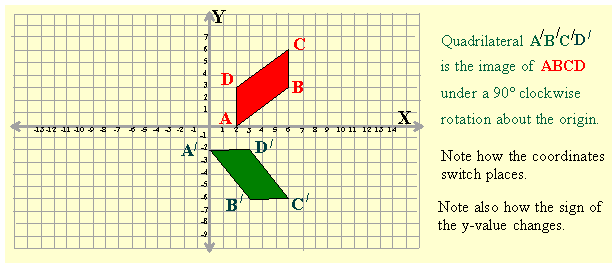
Example: A(2, 0); B(6, 3); C(6, 6) D(2, 3). Find the coordinates of the image vertices if quadrilateral ABCD is rotated 90° clockwise about the origin.
Solution: we must switch the coordinates and change the sign of the y-value (after the switch!!) because it is a clockwise rotation.
So the image vertices are A / (0, - 2); B / (3, - 6); C / (6, - 6); D / (3, - 2);
.
Rotations about the Origin of 180° and 270°
Let's take another look at the first diagram.
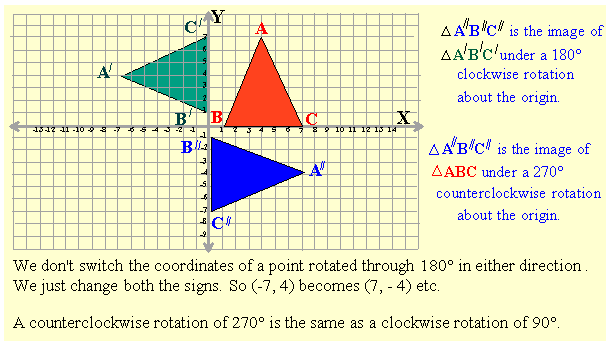
A Rotation changes the ORIENTATION of a figure.
When we inspect the relative positions of the green and blue triangles, the ones resulting from a turn of 180°, we see that we would get the same result if we had reflected the green triangle first in the x-axis and then in the y-axis. So, we can see that a rotation of 180° in either direction can be described as 2 consecutive reflections -- one vertical, one horizontal. And that's why we don't switch the coordinates, we just change both signs.
Summary
Rotations About the Origin
| Direction of Rotation | Angle of Rotation | Results on Coordinates |
| clockwise | 90° | ( x, y ) becomes ( y, - x ) |
| counterclockwise | 90° | ( x, y ) becomes ( - y, x ) |
| either way | 180° | ( x, y ) becomes ( - x, - y ) |
| clockwise | 270° | the same as counterclockwise 90° |
| counterclockwise | 270° | the same as clockwise 90° |
Now get a pencil, an eraser and a note book (graph paper), copy the questions,
do the practice exercise(s),then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
Practice
1) In the diagrams, the purple flag is the image of the green one
under a rotation about the indicated turn center. For each rotation, describe:
the degree measure of the angle and the direction (cw = clockwise, ccw = counterclockwise).

2) a) Draw triangle A(0, 0) B(2, 2) C(3, 0) and
rectangle D(0, - 2) E(3, - 2) F(3, - 1) G(0, - 1) on graph paper.
Find the coordinates of the vertices for both figures under a rotation about the origin of
| b) 180° counterclockwise | c) 90° clockwise | d) 270° clockwise |
e) Draw the image figures in blue and red as indicated.
3) State whether each of these statements is always true, or never true for rotations about the origin. Explain your answer if you choose never true.
a) When we rotate a figure about the origin, the image figure is larger than the original.
b) A 90° rotation moves the figure from one quadrant to another.
c) A rotation of 180° clockwise is the same as a 90° counterclockwise rotation.
d) A rotation of 180° in any direction is the same as two reflections.
e) A 90° clockwise rotation is the same as a 270° counterclockwise rotation.
4) Using the information in the summary, find the coordinates of the image vertices for
triangle A(- 1, 3) B(4, - 2) C(6, 5) under these rotations about the origin:
| a) 90° counterclockwise | b) 180° clockwise | c) 270° counterclockwise |
.
Solutions
1)
| a) 90° clockwise | b) 270° clockwise | c) 180° counterclockwise |
2) a) Draw triangle A(0, 0) B(2, 2) C(3, 0) and
rectangle D(0, - 2) E(3, - 2) F(3, - 1) G(0, - 1) on graph paper.
Find the coordinates of the vertices for both figures under a rotation about the origin of
| b) 180° counterclockwise A /(0, 0) B /(-2, - 2) C / (-3, 0) D /(0, 2) E / (-3, 2) |
c) 90° clockwise A /(0, 0) B /(2, -2) C /(0, -3) D /(- 2, 0) E /(-2, -3) |
d) 270° clockwise A /(0, 0) B /(-2, 2) C /(0, 3) D /(2, 0) E /(2, 3) |
e) check your drawing with the solutions in the table.
3)
a) never true. Rotations do not change the size of the figure, just the orientation.
b) Always true.
c) never true. A rotation of 180° clockwise is the same as a 180° rotation counterclockwise.
d) Always true.
e) Always true.
4) A(- 1, 3) B(4, - 2) C(6, 5)
| a) 90° counterclockwise A /(-3, -1) B /(2, 4) C / (-5, 6) |
b) 180° clockwise A /(1, -3) B /(-4, 2) C / (-6, -5) |
c) 270° counterclockwise A /(3, 1) B /(-2, -4) C / (5, -6) |
.
![]()
Analytic Geometry MathRoom Index