
means that the y coordinate approaches 7 as x approaches 2.
| ALGEBRAIC LIMITS |
| A LIMIT IS A Y-VALUE |
When we find a limit for an algebraic function, we find the value that y or f (x) APPROACHES as the x coordinate APPROACHES or gets extremely close to a given value.
NOTICE THE EMPHASIS ON THE WORD APPROACHES!!!
If y = 3x + 1 then

means that the y coordinate approaches 7 as x approaches 2.
In this case, y equals 7 when x = 2 because this linear function is defined at x = 2, so 2 is an element of the domain for y = 3x + 1.
Read "The Y's the Limit" -- article explaining limits.
| If f (a) exists then,
|
For this one, all we did was substitute x = 2, but when we get an indeterminate form by substitution, there is no precise y-value for the given x because the expression is undefined. To find the limit as x approaches a for an expression or function which is not defined at x = a, there are various techniques.
Factor, Reduce, Substitute
Example: find

since
 becomes
becomes
 at x = 2, it is an indeterminate form,
at x = 2, it is an indeterminate form,
so we find the value that y approaches as x approaches 2.

The graph of this function will have a hole -- a missing point at
 .
.
Since 2 is not an element of the domain,
 will be missing from the range.
will be missing from the range.
Note the form -- once we substitute x = a and evaluate, we no longer write "
 ".
".
Here's one where factoring is done by division.
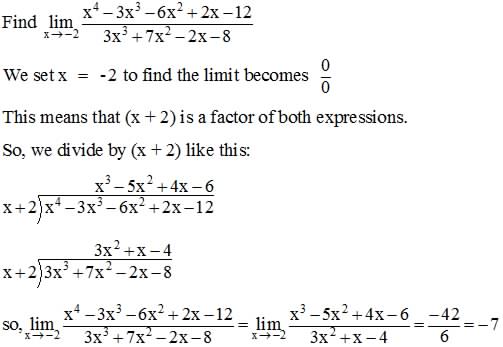
.
Rationalize, Reduce, Substitute
Find
 . If we set x = 4, we get
. If we set x = 4, we get
 , so we rationalize the numerator.
, so we rationalize the numerator.

As x approaches 4, the expression will approach
 . Since x cannot = 4, the expression will never be equal to
. Since x cannot = 4, the expression will never be equal to
 .
.
This one can be done using factor, reduce, substitute if we think of x as
 .
.

.
| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
To find
 when
when
 , we first do an analysis of the function on either
, we first do an analysis of the function on either
side of x = 4, since that's where the numerator changes sign. The only difference between the numerator and the denominator is the sign (+ or – ). The numerical value will be the same.
When x < 4, f (x) = – 1 (numerator is > 0 (abs. val. > 0) but denominator is < 0 since x < 4.)
When x > 4, f (x) = +1 (numerator is > 0 (abs. val. > 0) but denominator is > 0, since x > 4.)
In such a case, we discuss one-sided limits.
So, for
 , we define the left-side and right-side limits.(see diagram)
, we define the left-side and right-side limits.(see diagram)
 ..... and .....
..... and .....

Since ....
 , we say that
, we say that
 does not exist.
does not exist.
.
| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
Notation: A left limit is denoted
 -- notice the minus sign above the a in the subscript. A right limit is denoted
-- notice the minus sign above the a in the subscript. A right limit is denoted
 -- notice the plus sign above the a in the subscript.
-- notice the plus sign above the a in the subscript.
If f (x) is defined on the open interval (c, a) then the left-side limit means that f (x) gets very close to L 1, means that f (x) gets very close to L 1,as x gets very close to a, with x < a (approaching from the left of a). If f (x) is defined on the open interval (c, a), then the right-side limit |

| If f (x) is defined over an open interval including "a " except possibly at "a " itself then  exists and = L exists and = Lif and only if
|

.
| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
Functions Defined on Restricted Domains
For the function
 , the domain is [ – 3, 3] so we can only consider one-sided limits for the extremes of this function.
, the domain is [ – 3, 3] so we can only consider one-sided limits for the extremes of this function.
 and
and


 , x can only approach – 3 from above it (right-side limit) and x can only approach +3 from below it (left-side limit).
, x can only approach – 3 from above it (right-side limit) and x can only approach +3 from below it (left-side limit).| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
| A PIECEWISE DEFINED FUNCTION is one in which the function is defined differently on specific intervals or pieces of the domain. |
In this example the "pieces" are left of and right of x = 1. On the left of and at x = 1, we plot the linear function y = 2x – 1. Right of x = 1, we plot the parabola y = x².


 ..... and .....
..... and .....

 , therefore
, therefore
 exists and = 1.
exists and = 1..
However, if the function had been defined as:
 instead,
instead,
the left limit
 , but the right limit
, but the right limit
 .
.
The left limit is not equal to the right limit, so
 does not exist.
does not exist.
| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
Find the limits:
A/
1.a)
 |
b)
 |
c)
 |
d)
 |
2.a)
 |
b)
 |
c)
 |
|
3.a)
 |
b)
 |
c)
 |
d)
 |
.
B/ absolute value expressions
1.
 , , |
a)
 |
b)
 |
c)
 |
2.
 |
a)
 |
b)
 |
c)
 |
.
C/ one-sided limits
1. a)
 |
b)
 |
c)
 |
2.
 |
a)
 |
b)
 |
.
D/ piecewise defined functions
1. Let
 , find:
, find:
a)
 |
b)
 |
c)
 |
.
2. Let
 , find:
, find:
a)
 |
b)
 |
c)
 |
.
3. Let
 , find
, find

.
4. Let
 ,
,
a) find k so that f ( – 3) =

b) on the graph of f (x), what will the y-value be at the point where x = – 3?
.
| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
![]()
A/
1.a)
 ans: 22 |
b)
 ans: o |
c)
 = – 6 = – 6 |
d)
 ans:
|
2.a)
 ans: 3/4 |
b)
 ans: 0 |
c)
 ans: – 3 | |
3.a)
 factor, ans: 8 |
b)
 factor, ans: 12 |
c)
 factor, ans: 4 |
d)
 ans: 6 |
.
B/ absolute value expressions (DNE means does not exist -- no limit)
1.
 , , |
a)
 |
b)
 |
c)
 DNE DNE |
2.
 |
a)
 |
b)
 |
c)
 DNE DNE |
.
C/ one-sided limits
1. a)
 |
b)
 |
c)
 |
2.
 |
a)
 |
b)
 |
.
D/ piecewise defined functions
1. Let
 , find:
, find:
a)
 |
b)
 |
c)
 |
.
2. Let
 , find:
, find:
a)
 |
b)
 |
c)
 DNE DNE |
.
3. Let
 , find
, find

.
4. Let
 ,
,
a) find k so that f (–3) =


k should = – 6
b) on the graph of f (x), what will the y-value be at the point where x = – 3?
It will be – 6.
| algebraic limits | absolute value limits | one-sided limits | restricted domains |
| piecewise defined functions | practice | solutions |
![]()
(all content of the MathRoom Lessons © Tammy the Tutor; 2004 - ).