, then we can see immediately that there's a horizontal move of u1 units and a vertical move of u2 units -- since the initial point of the vector is the origin. In such a case, the vector is represented by the coordinates of the terminal point.
| VECTORS IN THE CARTESIAN PLANE |
Vectors in the Plane (R²)
Note: vectors are always displayed in vertical form in these lessons to
differentiate them from points. Vectors are bold text (u), scalars are italics (k).
Definition: A scalar or constant is a physical quantity that indicates only magnitude
Definition: A vector is a physical quantity that indicates both magnitude and direction.
Think of a wind speed -- say South -West at 20 kilometers/ hour.
The 20 km/h is the magnitude, and South-West is the direction.
Components of a 2-Dimensional Vector
Any 2-dimensional vector can be decomposed into its components -- which are the horizontal and vertical movement that make up the vector. If the vector is presented in the form
, then we can see immediately that there's a horizontal move of u1 units and a vertical move of u2 units -- since the initial point of the vector is the origin. In such a case, the vector is represented by the coordinates of the terminal point.
If we are given the coordinates of the initial and terminal points as (x1 , y1) and (x2 , y2) then its horizontal displacement is ( x2 – x1) and its vertical displacement is ( y2 – y1).
Example
If 
, we draw it by connecting the origin to the point (3, 1) so the components of this vector are 3 units horizontally and 1 unit vertically as shown.
If vector v is P1P2 with P1 = (1, 5) and P2 = (6, 9), then the horizontal or x component is 6 – 1 = 5 and the vertical or y component is 9 – 5 = 4. This vector is exactly the same as 
.
The Norm (length) of a Vector
|| u || denotes the norm of vector u
To find the length, norm or magnitude of a vector, we use the Pythagorean theorem.
The norm of vector u is 
. The norm of vector v is 
.
If u is a 2-dimensional vector, then Also, if P1 and P2 are the initial and terminal points, then |
The Direction or Angle of a Vector
We have found the norm or length of the vectors in our diagram, but what about the direction? This we describe in one of two ways. In a case like our example here, we use the angle between the vector and the horizontal axis to describe its direction. To accomplish this, we use a trig function. Generally, we use the Greek letter theta 
to denote the vector's angle.
For vector u, we know that 
. 
For vector v, we know that 
. 
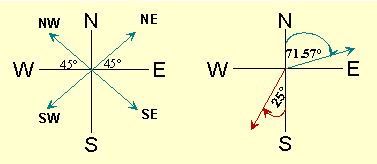
Since vectors are used in navigation, they are often described using the cardinal points of the compass -- North, East, South and West. In this case, the angle is most often determined by the vertical North/South axis and the vector.
In our example above, vector u would be designated N 71.57° E, since 71.57° is the complement of 18.43°. Similarly, vector v would be designated N 51.34° E, since 51.34° is the complement of 38.66°.
Angle descriptions presented this way instruct us how to move using the directions on a compass.
If we're told that vector u is N 71.57° E, we rotate 71.57° towards the East from due North.
If the direction of vector v is S 25° W, we rotate 25° towards the West from due South. Here's an image of these vectors.
If we're told the magnitude, (norm or length) of such a vector, we can find its components using trig on the right triangle the vector creates with the axes..
Example: Find the horizontal and vertical components of vectors u and v above if || u || = 7 cm and || v || = 5.3 km.
Solution:
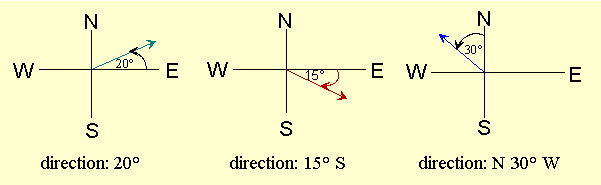
3 Ways to Describe the Direction of a Vector
1) If we're told an angle measure such as 20°, we measure the angle from the horizontal axis.
2) If we're told a direction and the angle, such as South 15°, we measure from the horizontal axis towards the given direction.
3) If we're told the angle between 2 directions, such as N 30° W, we measure from the first direction towards the 2nd direction. Here, we measure 30° towards the West from due North.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
Practice
1) Draw these vectors on a Cartesian Plane.
a) 4 cm, N 40° E ................... b) 10 km, S 20° W ................... c) 3 dm, horizontal, negative
d) 6 mi, direction 75° ............ e) 2.1 m/s, direction 210°.......... f) 4.5 km/h, vertical, negative
2) Find the norm of each vector.
a) u = (4, 2) ............ b) v = (3, – 3) ............ c) w = (– 2, – 6) .......... d) x = (– 2, 5)
3) Write the direction of each vector in # 2 in 2 different ways:
i) just an angle; ii) 2 directions and angle.
4) Describe each of the vectors shown here in 2 different ways:
5) Find the horizontal and vertical components of the vectors in question #4.
Solutions
1)
2) Find the norm of each vector.
a) 
...................... b) 
c) 
........... d)
3) Write the direction of each vector in # 2 in 2 different ways:
i) just an angle; ii) 2 directions and angle.
a) tan A = ½ therefore angle A = arctan ½ = 26.57°
The direction of vector u is i) 26.57° or ii) N 63.43° E.
b) Since x = y, the vector v is 45° below the x-axis in QIV so,
The direction of vector v is i) 315° or ii) S 45° E.
c) vector w is in QIII so, and tan A = 3. Since arctan 3 = 71.57°
The direction of vector w is i) 251.57° or ii) S 18.43° W.
d) vector x is in QII so, and tan A = 2.5. Since arctan 2.5 = 68.20°
The direction of vector w is i) 158.20° or ii) N 21.8° W.
4) Describe each of the vectors shown here in 2 different ways:
a) 3.2 m, N 50° E, ....or ....3.2 m, 40° .............. b) 2.4 cm, S 40° W ....or ....2.4 cm, 130°
c) 5 N, N 60° E,....... or .......5 N, 30° .............. d) 4 km/h, S 30° W ....or .... 4 km/h, 240°
5) a) x = 3.2 cos 40° = 2.45 m ............ y = 3.2 sin 40° = 2.06 m.
b) x = 2.4 cos 50° = 1.54 cm .............. y = 2.4 sin 50° = 1.84 cm.
c) x = 5 cos 30° = 4.33 N .................. y = 5 sin 30° = 2.5 N.
d) x = 4 cos 60° = 2 km/h .................. y = 4 sin 60° = 3.46 km/h.
( Linear Algebra MathRoom Index )
.