
| ANALYZING FIGURES in 1, 2 or 3 DIMENSIONS |
What's a Dimension and How Many are There?
The dictionary defines a dimension as " an extension in a line or direction ", such as length, width, or height. Most people think of a dimension as something we measure, so time fits the category. Until recently, we were taught that we live in a world of three dimensions – four, if we count time – and who doesn't count time? But now physicists tell us that our world really has 27 dimensions. In this lesson, however, we study geometric figures from the three comfortable dimensions we've lived in for centuries. We study the dimensions we call length, width, and height or altitude. We also investigate the number of points, lines or edges, and faces that make up these figures.

A One Dimensional Figure is an open plane figure that can be measured in only ONE way, such as length or width, but not both. These figures are lines, some of them straight, others curved, but they are all linear. They don't enclose a shape. We measure one dimensional figures with linear units such as inches, feet, yards, or miles. When you measure your height, you are measuring yourself in one dimension.

Two Dimensional Figures can be measured in TWO ways or directions, such as length AND width. These are closed plane figures like squares, circles or polygons of any shape or size. We measure 2 aspects of two-dimensional figures. The perimeter or distance around the outside, expressed in linear units; and the area or space enclosed by the perimeter expressed in square units.
The perimeter of a square with 7 inch sides is 4 × 7 or 28 inches.
The area of the same square is 7 × 7 or 49 square inches – written in².
Three Dimensional Figures are called solids. We measure them in three dimensions: length , width, and height or altitude. We use linear units for the perimeter, square units to measure the surface area, and cubic units to measure the volume or capacity of the solid.
There are two types of 3-dimensional solids:
those based on polygons, and those based on circles.
The first category includes prisms of all shapes.
The circular solids include cylinders, cones, and spheres.
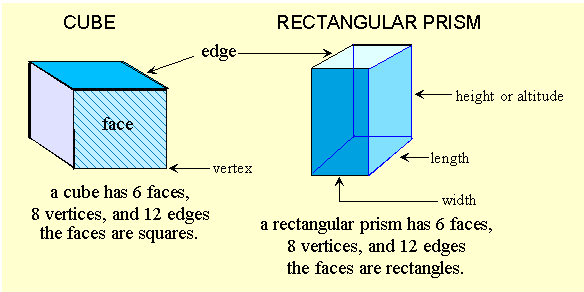
Polygonal solids are composed of polygon-shaped faces, vertices or points where more than 2 sides meet , and edges, the lines where two sides meet.
A prism has 2 identical or congruent bases shaped like a polygon.
A Prism is named for the shape of the base.
.
Let's Count Vertices, Edges and Faces
Though we could draw images of a three-dimensional solid and count the the vertices, edges and faces, there's a better way. We have developed formulas to find these numbers from the patterns we observed when counting them.
When the solid is a cube, rectangular prism, triangular prism or triangular pyramid:
If we know the number of FACES (F), to find the number of:
VERTICES (V): we multiply F by 2, then subtract 4: V = 2F - 4 = 2(F - 2)
EDGES (E): we multiply F by 3, then subtract 6: E = 3F - 6 = 3(F - 2)
If we know the number of EDGES (E), to find the number of:
VERTICES (V): we multiply E by 2, then divide by 3: V = 2E ÷ 3 = 2/3 E
FACES (F): we divide E by 3, then add 2: F = E ÷ 3 + 2
For a square pyramid with a square base and 4 triangular faces, the formulas are:
If we know the number of FACES (F), to find the number of:
VERTICES (V): we multiply (F - 2) by 2, then subtract 1: V = 2(F - 2) - 1 = 2F - 5 =
EDGES (E): we multiply (F - 2) by 3, then subtract 1: E = 3(F - 2) - 1 = 3F - 7
If we know the number of EDGES (E), to find the number of:
VERTICES (V): we multiply (E + 1) by 2, divide by 3 then subtract 1: V = 2/3(E + 1) - 1.
FACES (F): we divide (E + 1) by 3, then add 2: F = (E + 1) ÷ 3 + 2
| Solid | # of Faces | # of Vertices | # of Edges |
| Cube | 6 | 8 | 12 |
| Rectangular Prism | 6 | 8 | 12 |
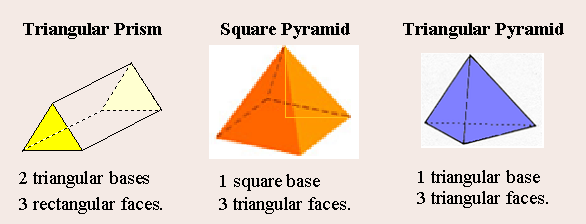
| Triangular Prism | 5 | 6 | 9 |
| Triangular Pyramid | 4 | 4 | 6 |
| Formula | F | V = 2(F - 2) | E = 3(F - 2) |
| Formula | F = E ÷ 3 + 2 | V = 2/3 E | E |
| Square Pyramid | 5 | 5 | 8 |
| Formula | F | V = 2(F - 2) - 1 | E = 3(F - 2) - 1 |
| Formula | F = 1/3 (E + 1) + 2 | V = 2/3(E + 1) - 1 | E |
.
Circular Solids
These solids are based on circles. Cans, the columns on buildings, and storage tanks for liquids, are cylindrical in shape. Detour indicators on the highway and dixie cups at the water fountain are cones, and the planet we live on as well as the toys we bounce, hit and throw are spheres.

 .
.

A cylinder has 2 flat surfaces and 1 curved surface.
A cone has 1 flat surface and 1 curved surface.
A sphere has only curved surfaces. We usually call a Sphere a ball or globe.
.
Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
.
Practice
1) Match the words on the left with the descriptions on the right.
| sphere | a) a rectangular prism with 6 square faces. |
| open plane figure | b) 3(F - 2) |
| rectangle | c) 1/3(E + 1) + 2 |
| cone | d) a 2-dimensional figure with 4 sides and angles. |
| square pyramid | e) can be measured in only one way. |
| cube | f) a circular solid with no flat surfaces. |
| formula for edges | g) a circular solid with one flat surface. |
| formula for faces | h) a 3-dimensional solid with 5 faces. |
2)

.
![]()
Solutions
1) Match the words on the left with the descriptions on the right.
| sphere | f) a circular solid with no flat surfaces. |
| open plane figure | e) can be measured in only one way. |
| rectangle | d) a 2-dimensional figure with 4 sides and angles. |
| cone | g) a circular solid with one flat surface. |
| square pyramid | h) a 3-dimensional solid with 5 faces. |
| cube | a) a rectangular prism with 6 square faces. |
| formula for edges | b) 3(F - 2) |
| formula for faces | c) 1/3(E + 1) + 2 |
2)
a) The base is a rectangular prism with no top -- so, it has 6 - 1 = 5 faces.
b) Because there is no top, it has ½ the number of vertices it should, so it has 4 vertices on the ground. Recall that a vertex is a point where MORE THAN 2 SIDES meet.
c) The roof is a triangular prism missing 1 rectangle, it has no bottom -- so it has 4 faces -- 2 triangles front and back and 2 rectangles -- the sides of the roof.
d) The roof is attached to the base so it loses 2 edges at the front and rear. It has 9 - 2 = 7 edges.
.
![]()