| SIMILAR SOLIDS |
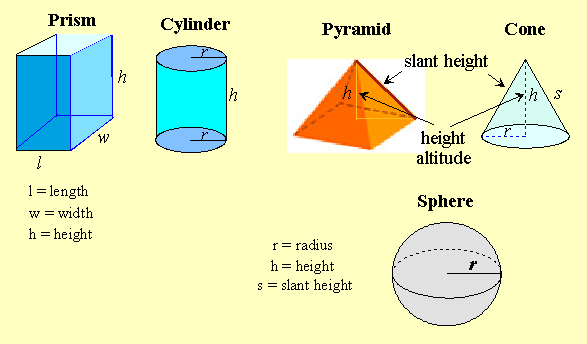
Naming the Dimensions
We've already learned in our work with 2-dimensional similar figures that
The ratio of the sides is called the proportionality factor.
We generally use c or k to represent it because
it can be called the proportionality CONSTANT.
We also learned that:
In similar figures, the ratio of the perimeters is equal to the ratio of the sides.
and
The ratio of the areas is equal to the square of the ratio of the sides.
In 2-dimensions, we name the "sides" of the figure with familiar words such as length, width, base, height, etc. When we discuss 3-dimensional solids, we use the same terms as well as others.
The vertical height of a 3-dimensional solid is also called the altitude. Solids that come to a point like cones and pyramids have a slant height which is never called the altitude.
We'll use a diagram to study the shapes and the names of their dimensions.

Descriptions and Formulas
Let's describe these solids and investigate the formulas for their surface area and volume.
Rectangular Prism: is a pile of rectangles. It has 6 rectangular faces.
Surface Area = 2( lw + lh + wh ), Volume = l × w × h
Cylinder: is a pile of circles. It has 2 circular faces, one rectangular "side"
Surface Area =  , Volume =
, Volume = 
Pyramid: shape depends on the shape of the base. Faces meet at a point called vertex or apex.
Surface Area = sum of the areas of faces, Volume =  Area of base × height.
Area of base × height.
Right Circular Cone: has a circular base, curved sides and a point called vertex or apex.
Surface Area =  , Volume =
, Volume = 
Sphere: surface is 4 circles, volume is 4 cones. It has a single curved surface.
Surface Area =  , Volume =
, Volume = 
Note:
for straight sided solids (prisms, cylinders): Volume = (area of base) × height
for pointy slanted sided solids (pyramids, cones): Volume =  (area of base) × height
(area of base) × height
Similarity in the 3rd Dimension
When we study similar solids in 3-dimensions, we find that the ratio of their volumes is the cube of the ratio of their "sides" (or dimensions)
In similar solids:

The level one ratio -- that of the sides or dimensions -- determines the other two.
Note: We usually say "area" instead of surface area -- but we mean surface area.
Example
Use the data in the diagram to find the dimensions and volume of the larger prism.

Example
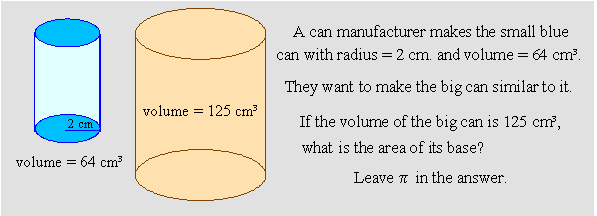
We know the volume of both cans, so we know the level 3 ratio of 125 : 64.
It is the cube of the level 1 ratio (that of the radii), so we take the cube root.

This means the level 1 ratio of BIG RADIUS to small radius is 5 to 4.
We know r = 2 cm. so

and now we find the base area of the big can

We could find the area of the small base then multiply it by 25/16 -- the square of 5/4.
If we know level 3 and need level 2 -- we take the cube root then square the result.
Caution: Watch for statements like "the area of the larger is 4 times the area of the smaller". It tells us the level 2 ratio of 4 : 1.
In this example, we knew the level 3 ratio and the radius of the small can, which is a level 1 value. Once we take the cube root of the level 3 ratio, we use it to get to the level 2 ratio or area.
Example: The Listenup Company makes audio speakers in 2 sizes. The speakers are similar rectangular prisms. The small one is 40 cm high, its base area is 250 cm². The area of the larger speaker's base is 490 cm². Find the height and volume of the larger speaker?

Now get a pencil, an eraser and a note book, copy the questions,
do the practice exercise(s), then check your work with the solutions.
If you get stuck, review the examples in the lesson, then try again.
![]()
Practice
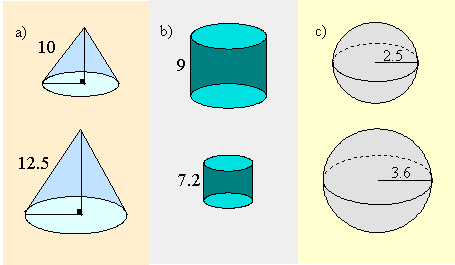
1) For these solids find the "BIG to little" ratio of the sides, surface areas, and volumes.
Make a diagram for questions 2, 3 and 4.
2) A company makes 2 similar cylindrical vases.
The smaller one has a diameter of 10 cm. and a height of 20 cm.
The total area of the larger vase is 4 times that of the smaller.
Find the dimensions and volume of the larger vase.
3) Two right prisms with rectangular bases are similar.
The base area of the smaller is 3.14 cm² and its height is 1.5 cm.
The base area of the larger is 78.5 cm².
What is the volume of the larger prism rounded to the nearest unit?
4) Two cylindrical food cans are similar.
The diameter of the smaller can equals the radius of the larger can.
How many of the smaller cans could we fill with the full contents of the larger one?
5)

![]()
.
Solutions
1)
| ratio | sides | surface area | volume |
| a) |  |
25 : 16 | 125 : 64 |
| b) |  |
25 : 16 | 125 : 64 |
| c) |  |
36² : 25² | 36³ : 25³ |
2) h = 40 cm, r = 10 cm and volume = 12566 cm³.
3) 
4) The level 1 ratio is 2 : 1, so the ratio of volumes is 2³ : 1 = 8 : 1
We could fill 8 small cans with the contents of the larger one.
5) The level 1 ratio is 5 : 20 or ¼, so the level 3 ratio = (¼)³.
The volume of each small piece will be 1/64 th the volume of the mother piece.
4800 ÷ 64 = 75 cm³.
![]()